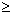 1, b
1, b 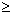 1
that satisfy the equation
1
that satisfy the equation
Version: English
Second day
Mar del Plata, Argentina - July 25, 1997
4
An n x n matrix (square array) whose entries come from the set S = {1, 2, ... , 2n - 1}, is called a silver matrix if, for each i = 1, ... , n, the ith row and the ith column together contain all elements of S. Show that
(a) there is no silver matrix for n = 1997;
(b) silver matrices exist for infinitely many values of n.
5
Find all pairs
(a,b)
of integers
a 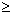 1, b
1, b 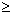 1
that satisfy the equation
1
that satisfy the equation
a(b2) = ba.
6
For each positive integer n , let f(n) denote the number of ways of representing n as a sum of powers of 2 with nonnegative integer exponents.
Representations which differ only in the ordering of their summands are considered to be the same. For instance, f(4)=4, because the number 4 can be represented in the following four ways:
4; 2+2; 2+1+1; 1+1+1+1.
Prove that, for any integer
n 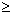 3:
3:
2n2/4 < f(2n) < 2n2/2.