![[ IOI Home page ]](../logo.gif) Task 1-1: Packing Rectangles
Task 1-1: Packing Rectangles![[ IOI Home page ]](../logo.gif) Task 1-1: Packing Rectangles
Task 1-1: Packing Rectangles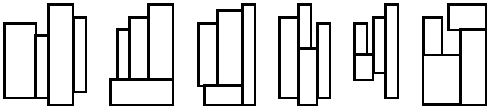
Four rectangles are given. Find the smallest enclosing (new) rectangle into which these four may be fitted without overlapping. By smallest rectangle we mean the one with the smallest area.
All four rectangles should have their sides parallel to the corresponding sides of the enclosing rectangle. Figure 1 shows six ways to fit four rectangles together. These six are the only possible basic layouts, since any other layout can be obtained from a basic layout by rotation or reflection.
There may exist several different enclosing rectangles fulfilling the requirements, all with the same area. You have to produce all such enclosing rectangles.
_____________ ______________ | INPUT.TXT | | OUTPUT.TXT | |___________| |____________| | 1 2 | | 40 | | 2 3 | | 4 10 | | 3 4 | | 5 8 | | 4 5 | |____________| |___________|Figure 2: Example input and output