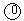Polygon
Polygon is a game for one player that starts on a polygon with N vertices, like the one in
Figure 1, where N=4. Each vertex is labelled with an integer and each edge is labelled with
either the symbol + (addition) or the symbol * (product). The edges are numbered from 1 to N.
Figure 1. Graphical representation of a polygon
On the first move, one of the edges is removed.
Subsequent moves involve the following steps:
- pick an edge E and the two vertices V_1 and V_2 that are linked by E; and
- replace them by a new vertex, labelled with the result of performing the operation indicated in E on the labels of V_1 and V_2.
The game ends when there are no more edges, and its score is the label of the single vertex remaining.
Sample game
Consider the polygon of Figure 1. The player started by removing edge 3. The effects are depicted in Figure 2.
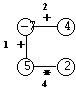
Figure 2. Removing edge 3
After that, the player picked edge 1,

Figure 3. Picking edge 1
then edge 4,

Figure 4. Picking edge 4
and, finally, edge 2. The score is 0.
Figure 5. Picking edge 2
Task
Write a program that, given a polygon, computes the highest possible score and lists all the edges that,
if removed on the first move, can lead to a game with that score.
Input Data
File POLYGON.IN describes a polygon with N vertices. It contains two lines.
On the first line is the number N.
The second line contains the labels of edges 1, ..., N, interleaved with the vertices'
labels (first that of the vertex between edges 1 and 2, then that of the vertex between edges 2 and 3, and so on,
until that of the vertex between edges N and 1), all separated by one space. An edge label is either the letter
t (representing +) or the letter x (representing *).
Sample Input
4
t -7 t 4 x 2 x 5
This is the input file for the polygon of Figure 1. The second line starts with the label of edge 1.
Output Data
On the first line of file POLYGON.OUT your program must write the highest score one can get for the input
polygon.
On the second line it must write the list of all edges that, if removed on the first move, can lead to a game
with that score.
Edges must be written in increasing order, separated by one space.
Sample Output
33
1 2
This must be the output file for the polygon of Figure 1.
Constraints
3 <= N <= 50
For any sequence of moves, vertex labels are in the range [-32768,32767].