8th International Olympiad in Informatics, Veszprém, Hungary
IOI'96 Day 1
Problem 2: Job Processing
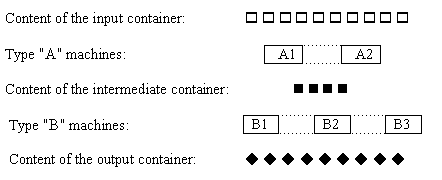
Figure 1
A factory is running a production line. Two operations have to be performed on each job: first operation "A", then operation "B". There is a certain number of machines capable of performing each operation. Figure 1 shows the organisation of the production line that works as follows. A type "A" machine takes a job from the input container, performs operation "A" and puts the job into the intermediate container. A type "B" machine takes a job from the intermediate container, performs operation "B" and puts the job into the output container. All machines can work in parallel and independently of each other, and the size of each container is unlimited. The machines have different performance characteristics, a given machine works with a given processing time.
Give the earliest time operation "A" can be completed for all N jobs provided that the jobs are available at time 0. (Subtask A). Also compute the minimal amount of time that is necessary to perform both operations on N jobs (Subtask B).
Input Data
The file INPUT.TXT contains positive integers in five lines. The first line contains N, the number of jobs (1<=N<=1000). On the second line, the number M1 of type "A" machines (1<=M1<=30) is given. In the third line there are M1 integers, the job processing times of each type "A" machine. The fourth and the fifth line contain the number M2 of type "B" machines (1<=M2<=30) and the job processing times of each type "B" machine, respectively. The job processing time is measured in units of time, which includes the time needed for taking a job from a container before processing and putting it into a container after processing. Each processing time is at least 1 and at most 20.
Output Data
Your program should write two lines to file OUTPUT.TXT. The first line should contain one positive integer: the solution of subtask A. The second line should contain the solution of subtask B.
Example Input and Output
Figure 2 gives a possible input file and the corresponding output file.
INPUT.TXT
5
2
1 1
3
3 1 4
OUTPUT.TXT
3
5
Figure 2
