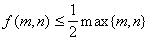Version: English

First day
Mar del Plata, Argentina - July 24, 1997

1

In the plane the points with integer coordinates are the vertices of unit squares. The squares are coloured alternately black and white (as on a chessboard).

For any pair of positive integers m and n, consider a right-angled triangle whose vertices have integer coordinates and whose legs, of lengths m and n, lie along edges of the squares.

Let S₁ be the total area of the black part of the triangle and S₂ be the total area of the white part. Let

f(m,n) = | S₁ - S₂ |.

(a) Calculate f(m,n) for all positive integers m and n which are either both even or both odd.

(b) Prove that 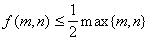for all m and n.

(c) Show that there is no constant C such that f(m,n) < C for all m and n.

2

Angle A is the smallest in the triangle ABC.

The points B and C divide the circumcircle of the triangle into two arcs. Let U be an interior point of the arc between B and C which does not contain A.

The perpendicular bisectors of AB and AC meet the line AU at V and W, respectively. The lines BV and CW meet at T.

Show that

AU = TB + TC.

3

Let x₁, x₂, ... , x_n be real numbers satisfying the conditions:

|x₁ + x₂ + ... + x_n | = 1

and

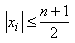for i = 1, 2, ... , n.

Show that there exists a permutation   y₁, y₂, ... , y_n  of   x₁, x₂, ... , x_n  such that

.
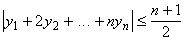